지우너
[한정현 컴퓨터 그래픽스] 강의소개, 1, 2강 본문
본 글은 한정현 교수님의 "컴퓨터 그래픽스" 강의를 정리한 글입니다(강의에 사용된 ppt 링크).
3차원 컴퓨터 그래픽스의 정의
3차원으로 표현된 물체를 입력으로 받아서 2차원 영상을 출력하는 작업. 그런 2차원 영상을 프레임(frame) 이라고도 이야기 함
영화고 게임에서처럼 연속적으로 프레임을 보여 주면 물체의 움직임을 표현 가능
프레임을 얼마나 빨리 만들어 내는가에 따라서 실시간 그래픽스 / 비실시간 그래픽스로 구분
실시간 그래픽스의 대표는 게임, 가상현실, 증강현실 등
보통 초당 30개 이상의 프레임을 만들어 내야 되는데, 그런 것들을 frames per second(=fps) 라고 이야기.
비실시간 그래픽스는 영화에서 쓰이는 특수효과
영화의 특수 효과의 대개 목표는 실사 영상 과 구분이 되지 않는 사진 사실적인 영상을 만들어내는 것
⟹ 상당히 많은 연산을 수행. 뭐 몇 분에서 몇 시간까지 걸리는건 뭐 일반적인 거고, 아주 고급스러운 영상을 만들어 낼 땐 하루 종일 시간을 소요
실시간 그래픽스와 비실시간 그래픽스를 구분할 때, 실제로 양쪽에서 쓰이는 알고리즘과 기법들은 상당히 다를 수가 있다.
이번 수업에스는 OpenGL ES를 이용해 실시간 그래픽스의 기본적인 알고리즘들을 설명
컴퓨터 그래픽스(실시간 / 비실시간 공통)는 보통 다섯 단계로 구분

모델링-리깅-애니메이션 이 3단계는 보통 그래픽 아티스트 또는 그래픽 디자이너 라고 하는 사람들이 오프라인에서 수행
최종적으로 애니메이션이 생성되면, 그 애니메이션을 실시간 재생하고, 그 다음에 렌더링을 수행한 다음, 필요에 따라 포스트 프로세싱을 수행 (애니메이션-렌더링-포스트프로세싱은 런타임에 컴퓨터 프로그램이 자동으로 실행하여 이루어짐)
- 1단계: Modeling
모델: 컴퓨터가 이해하고 처리할 수 있는 형태로 물체를 표현한 것
모델링: 모델을 만들어내는 작업의 총칭

실시간 그래픽스에서는 대개의 경우 폴리곤 메쉬, 다각형 메쉬를 사용
야구공을 자세히 보면 다각형들이 그물처럼 촘촘하게 엮여 있는 것을 볼 수가 있는데, 이런 의미에서 풀리고 매쉬 라고 얘기
다각형 중에 가장 간단하게 삼각형이라서, 삼각형 메쉬가 가장 널리 쓰이고 있다.
모델링 단계에서는 이렇게 폴리곤 메쉬와 폴리곤 메쉬에 입힐 텍스처를 만든다.

야구 선수가 있을 때, 야구선수의 표면이 펼쳐진 이미지들을 위와 같은 형태로 만들어 낸다.
오프라인에서 그래픽 아티스트가 이러한 이미지 텍스처를 만들면 런타임에 폴리곤 메쉬 표면에 입혀져서 영상을 만들어 낸다.
이런 작업들 이제 텍스처링이라고 한다.
모델링 단계에서는 3차원 폴리곤 메쉬를 만들고 텍스처를 만들어야 된다 정도를 이해하면 될 것 같다
- 2단계: Rigging_애니메이션을 위해 뼈와 메쉬의 상관 관계를 정의해주는 작업

야구 선수가 공을 치고, 달리고, 슬라이딩 하는 등의 움직임을 표현해야 한다,.
가장 기본적인 방법은 뼈로 구성된 골격을 사용하는 것.
그렇게만 뼈가 있다고 할 때 그러한 뼈를 아까 만든 폴리곤 메쉬 안에 집어 넣는다.
그 후 폴리곤 메쉬를 구성하는 꼭지점과 뼈의 상관관계를 잘 정의해주면, 위처럼 팔을 들었을 때, 팔 가까이에 있는 폴리곤 메쉬가 움직이게 된다. 이게 애니메이션.
리깅은 애니메이션을 위해서 뼈를 만들고 뼈와 폴리곤 메쉬의 상관 관계를 정하는 작업. 그래픽 디자이너가 모델링과 리깅을 수행하고, 리깅이 수행되면 애니메이션을 만들 수 있다.
- 3단계: Animation
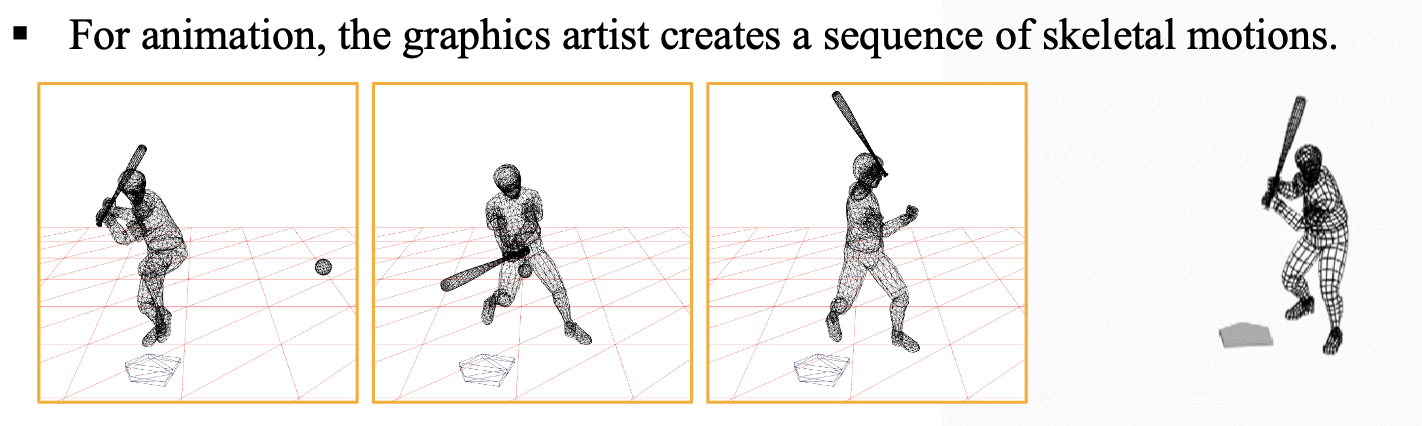
뼈를 이용한 애니메이션을 만들고 싶어서 스켈레톤 모션을 정한다.
오프라인 단계에서 이렇게 스켈레톤 모션을 만들면 런타임에 는 기본적으로 그 애니메이션이 재생이 되는 것
이렇게 그래픽 아티스트가 모델링-리깅-애니메이션 세 가지 작업을 수행
이것들 위한 도구들이 나와있는데, 맥스 마야 같은 프로그램이 있다.
여기까지 그래픽아티스트/그래픽 디자이너의 작업이 끝났다.
- 4단계: Rendering
그 다음에는 컴퓨터 프로그램이 런타임에 만들어진 모델을 애니메이트 시켜야 된다.
그러기 위해서는 기본적으로 애니메이션 재생하고 렌더링 작업을 수행을 해야 함.
렌더링: 3차원 광경으로부터 2차원 영상을 만들어 내는 것
사실적인 렌더링(Realistic rendering)은 텍스처링(texturing)뿐만 아니라 라이팅(lighting)이 필수 요소인 복잡한 프로세스.

라이팅은 빛과 물체의 상호작용. 텍스쳐링을 해서 야구선수가 만들어져도 실제 빛이 어디서 오느냐에 따라 그림자가 위와 같이 만들어지는 등의 작업이 수행되어야 한다.
- 5단계: Post-Processing
포스트 프로세싱(=후처리)은 선택적으로 수행된다.
우리가 동영상을 볼 때도 빠르게 움직이는 물체는 흐릿한 영상을 만들어 낸다. 실시간 그래픽스에서도 그러한 그 흐릿한 움직임 모션 블러(motion blur)를 만들어내면 영상이 굉장히 사실적으로 보인다. 빠르게 움직이 있는 야구 베트를 흐릿하게 만들어 사실성을 높이는 것이 후처리 과정의 대표적인 예시.
하지만 뭐 앞의 렌더링과 달리 포스트 프로세싱은 필수적인 작업은 아니기 때문에 선택적으로 수행할 수 있다.
모델링-리깅-애니메이션-렌더링-포스트프로세싱으로 구성되는 그래픽스 제작 단계를 살펴봤다.
앞의 3가지 단계는 오프라인에서 Maya, 3ds Max and Blender 같은 것을 이용하여 그래픽 아티스트가 수행하고, 그렇게 만들어진 애니메이션을 재생하고 렌더링하고 후처리를 하는 것은 컴퓨터 프로그램이 수행한다.

게임과 같은 경우에는 게임 엔진 이라고 하는 개발 툴(유니티, 언리얼 등)을 많이 사용
게임 엔진은 굉장히 많은 기능을 갖고 있는 개발도구. 그러한 기능들 중에 애니메이션 재생, 렌더링, 후처리 작업들이 다 포함
게임 엔진 아래에는 뭐가 있는가 →그래픽스 인터페이스

대표적인 인터페이스가 마이크로소프트의 Direct3D와 크로노스(Khronos)의 OpenGL
OpenGL 밑에는 뭐가 있느냐 →GPU
CPU: central processing unit
GPU: graphic processing unit
그래픽 API는 3D 애플리케이션이나 게임 엔진에 텍스처링과 같은 필수 그래픽 기능을 제공.
오늘날 이러한 기능은 GPU(그래픽 처리 장치)에서 구현된다.
게임 엔진 이라든가 그래픽스 애플리케이션이 OpenGL ES를 호출할 때는 실행 OpenGL ES는 GPU를 가동을 하게 된다.
OpenGL ES는 한마디로 GPU의 소프트웨어 인터페이스로 간주할 수 있다. API는 애플리케이션의 그래픽 명령을 GPU에서 실행할 수 있는 명령어로 변환합니다.
이 강의에서는 실시간 그래픽의 핵심 알고리즘이 OpenGL ES에서 어떻게 구현되는지 소개합니다. 이러한 알고리즘은 게임 엔진에 없어서는 안 될 필수 요소입니다.
그래픽스는 비교적 수학을 많이 필요로 하는데, 학부 수준의 컴퓨터 그래픽스에서는 선형 대수의 기초적인 내용(행렬, 벡터)만 알면 됨
m 개의 행이 있고 n개의 열이 있을 때, 행렬의 사이즈는 mXn
m=n이면 square matrix(정사각 행렬)이라고 한다.
두가지 행렬이 주어졌을때 곱하는 것은 뭐 첫번째 행을 따고 첫 번째 열을 따서 쌍쌍이 곱해서 더하면 원소가 만들어지고,
다시 첫 번째 행을 따고 두 번째 열을 따서 똑같이 쌍쌍이 곱하면 원소가 만들어진다.
이런 일을 반복을 하면 전체 행렬 곱셈이 완성된다.
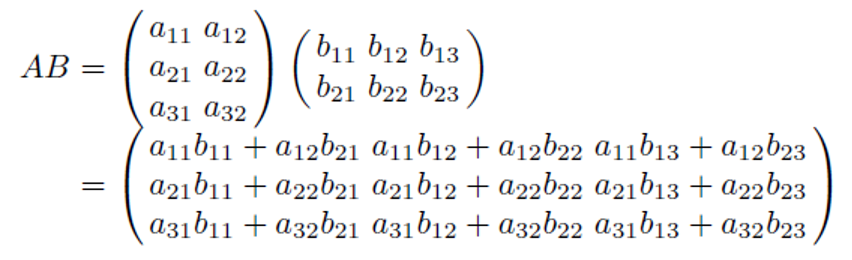
a 행렬의 크기를 lXm 이라고 하고, b 행렬의 크기를 mXn라고 하면, m이 동일 → 두 행렬의 곱셈이 가능
결과로 산출되는 행렬의 크기는 lXn
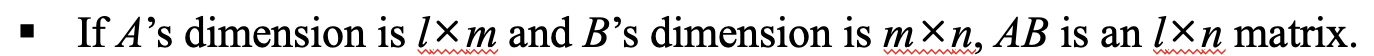
벡터
2차원 벡터(x, y) 3차원 벡터 (x, y, z)로 표현이 되는데, 이런 것들을 기본적으로 row vector라고 말한다.
각각의 좌표를 열(column)의 형태로 쓸 수 있는데, 이를 column vector라고 한다.
근데 사실 벡터라고 하는 것은 특별한 행렬이라고 할 수 있다.
1. Matrix-vector multiplication 이렇게 2차원 벡터가 있을 때, M은 3X2, v는 2X1니까 곱셈이 가능하다.
M의 행 a, b와 v의 열 x, y를 곱하면 첫 번째 원소, M의 두 번째 행 c, d와 v의 첫번째 열 x, y를 곱해서 두 번째 원소
마지막으로 M의 마지막 행 e, f와 v의 첫번째 열 x, y를 곱하면 3번째 원소가 나온다.
3X2 행렬과 2X1 행렬을 곱했기 때문에 결과로 나오는 행렬의 크기는 3X1이 된다.

2. Transpose denoted by M^T 1의 M column은 ace / bdf로 정의가 되는데 얘들을 행으로 바꿔보자. 이를 전치행렬(Transpose)이라고 한다.
3. A different way of matrix-vector multiplication v전치행렬과 M전치행렬을 곱해보자
그러면 앞의 행렬은 1X2, 뒤의 행렬은 2X3 사이즈라서 1X3 사이즈 행렬 즉, 3차원 벡터가 만들어진다.
따라서 행렬(M, Matrix의 약자)과 벡터(v, Vector의 약자)를 곱셈했을 때 그 결과는 행렬의 Transpose를 취하고, 벡터의 Transpose를 취한 것 과 같다.
물론 1에서는 열벡터(column vector)로 결과가 나오고, 3에서는 행벡터(row vector)의 결과가 나왔다. 어떻게 행렬 벡터의 곱셈을 표현하는가의 차이
행렬-벡터 곱셈의 경우,
OpenGL은 열백터(column vector)를 사용하고, 1처럼 행렬의 오른쪽에 벡터가 놓여져서 곱셈이 이루어진다.
Direct3D는 행벡터(row vector)를 사용하고, 3처럼 행렬의 왼쪽에 벡터가 놓이게 된다.
우리는 OpenGL을 사용하므로, 1의 표현법을 따를 것이다

1. Identity matrix denoted by I 단위행렬(Identity matrix)
대각선쪽(Diagonal)의 원소가 모두 1이고, 나머지 원소는 모두 0인 경우, I(Identity의 약자?)라고 표현한다
2. For any matrix M, MI = IM = M. 단위행렬의 특징 어떤 행렬과 곱하든 그 행렬을 유지한다는 것.
3. 두 행렬 AB를 곱해서 단위행렬이 만들어진 경우, B는 A의 역행렬이라고 하고 A^{-1}이라고 표현한다.
마찬가지로, A도 B의 역행렬이고, B^{-1}이라고 표현할 수 있다.
4. Theorems
4-1. 두 행렬 AB를 곱한 결과의 역행렬은 B역행렬과 A역행렬을 곱한 것과 동일하다.
4-2. 마찬가지로 AB를 곱한 결과에 전치행렬(열과 행을 바꾸는 것)을 취하면, B의 전치행렬과 A의 전치행렬을 곱한 결과와 동일하다.

1. 2차원 3차원 벡터의 좌표는 위와 같이 아래첨자 x, y / x, y, z를 이용하여 표현.
2. 그런 벡터의 크기는 2에 나온 것처럼 표현된다(두 점 사이의 거리 공식 떠올리기).
3. 주어진 벡터를 자기 자신의 길이로 나누는 과정을 정규화(normalization)라고 이야기 함.
4. 정규화를 통해서 만들어진 벡터의 길이는 항상 1이다. 이를 단위벡터(unit vector)라고 함.
이상으로 행렬과 벡터의 기초에 대해 살펴보았다. 본격적으로 그래픽스에 필요한 수학을 조금 더 들어가보자.
- 2차원

1. Coordinate system=origin+basis 좌표계(Coordinate System)는 원점(origin)과 기저(basis)로 정의함
2. 그래픽스에서는 좌표계를 간단하게 공간이라고도 함.
3. 2차원 공간은 x축과 y 축으로 정의가 된다. 2D 공간에서 모든 벡터는 기저 벡터의 선형 조합으로 정의할 수 있다.
e_1: x축에 나란하면서 길이가 1인 벡터, e_2: y축에 나란하면서 길이가 1인 벡터
e_1과 e_2는 standard basis가 된다. 왜 basis라고 하냐면, e_1, e_2를 기저(basis)로 삼아서 2차원 공간에 있는 모든 벡터를 선형 조합의 형태로 표현할 수 있기 때문
예를 들어(3, 5)라는 좌표를 갖는 벡터를 생각해보자.
(3의 왼쪽 그림) 그러면 e_1에다가 3을 곱하고, e_2에 5를 곱해서 더하면(e_1과 e_2를 3과 5라는 계수를 가지고 선형 조합을 하면) 우리가 원하는 (3, 5)라는 벡터를 얻을 수 있다.
→standard basis는 정규직교(orthonormal, orthogonal+normalized)하다는 특성을 갖고 있다. e_1과 e_2는 90도를 이루면서, 단위벡터이다.
(3의 가운데 그림)그런데 (3, 5)라는 벡터를 만드는 다른 방법도 있다. (1, 1)과 (0, 2)라는 basis가 주어졌다고 생각해보자. (1, 1)에 3을 곱하고, (0, 2)에 1을 곱해서 더하면 즉, (1, 1)과 (0, 2)를 각각 3과 1이라는 계수를 써서 선형 조합을 하면 (3, 5)라는 벡터가 만들어진다.
→(1, 1)과 (0, 2)도 완벽한 basis의 역할을 함. 하지만 x축, y축과 나란히 있는 e_1, e_2와는 다르기 때문에 standard basis는 아니다. 각도가 90도가 아니고(non-orthogonal), 각각의 크기도 1이 아니다(non-normalized).
(3의 오른쪽 그림) 비록 standard는 아니지만 정규직교(orthonormal)하는 벡터를 우리는 상상할 수 있다.
기저(basis)와 정규직교 기저(orthonormal basis)의 개념은 아주 중요!!
- 3차원

1. 2차원에서 e_1과 e_2가 standard basis를 구성했는데 3차원은 e_3라는 새로운 벡터가 추가되어 {e_1, e_2, e_3}가 3차원 standard basis를 구성한다. 즉, e_1, e_2, e_3의 선형 조합을 통해 3차원 공간에 있는 모든 벡터를 다 표현할 수 있다는 것.
2. 당연히 이 standard basis도 orthonormal하다.
3. 2차원처럼 3차원에서도 e1, e2,e3 외에 다양한 orthonormal basis가 있다.
4. All 2D and 3D bases presented from now on will be orthonormal by default. 지금부터 말하는 bases는 모두 orthonormal한 것으로 국한한다.
벡터 연산_Dot Product = Inner Product = 내적
내적의 결과값은 항상 스칼라 값이 나온다.

1. a와 b를 n차원 벡터라고 생각해보자.
(a1, a2, a3, ..., an), (b1, b2, b3, ..., bn) 각각 이렇게 좌표를 표현할 수 있다. 이때 내적(Dot Product)은 A⋅B로 표기.
정의는 a와 b에 해당되는 좌표를 모두 곱해서 더한 것.
2. 대수공식의 기하학적 해석(정의): ‖a‖‖b‖cosθ, θ는 A와 B사이의 각도.
(그림1) (0, 1)⋅(1, 0)은 각각의 x좌표 0, 1과 y좌표 1, 0을 곱해서 더한 값 = 0*1 + 1*0 = 0 <- 내적의 대수적인 정의. 대수적 정의와 기하학적 정의 2개가 있는 셈인데, 당연히 그 값은 같아야 한다. 2번째 정의를 이용해보면 a의 크기, b의 크기, cosθ를 하면 되는데, 사실 a, b의 크기는 크게 의미가 없다. cosθ가 각도가 90도니까 곧바로 0이 되기 때문. 대수적 정의에서의 답이었던 0과 동일.
⇒ 2-1. 여기서 알 수 있는 것: 두 개의 벡터가 수직을 이룰 때, 그 길이에 상관없이 내적 값은 0이 된다는 것.
(그림2) 두 벡터 사이의 각도가 예각인 경우: 내적의 결과는 양수가 나온다. (1, 1)과 (1, 0)을 내적시키면 각각의 x좌표 1, 1과 y좌표 1, 0을 곱해서 더한 값 = 1*1 + 1*0 = 1
(그림3) 두 벡터 사이의 각도가 둔각인 경우: 내적의 결과는 음수가 나온다. (-1, 1)과 (1, 0)을 내적시키면 각각의 x좌표 -1, 1과 y좌표 1, 0을 곱해서 더한 값 = -1*1 + 1*0 = -1
기하적으로도 θ가 90도를 넘어가는 순간 cos는 음수가 되기 때문.
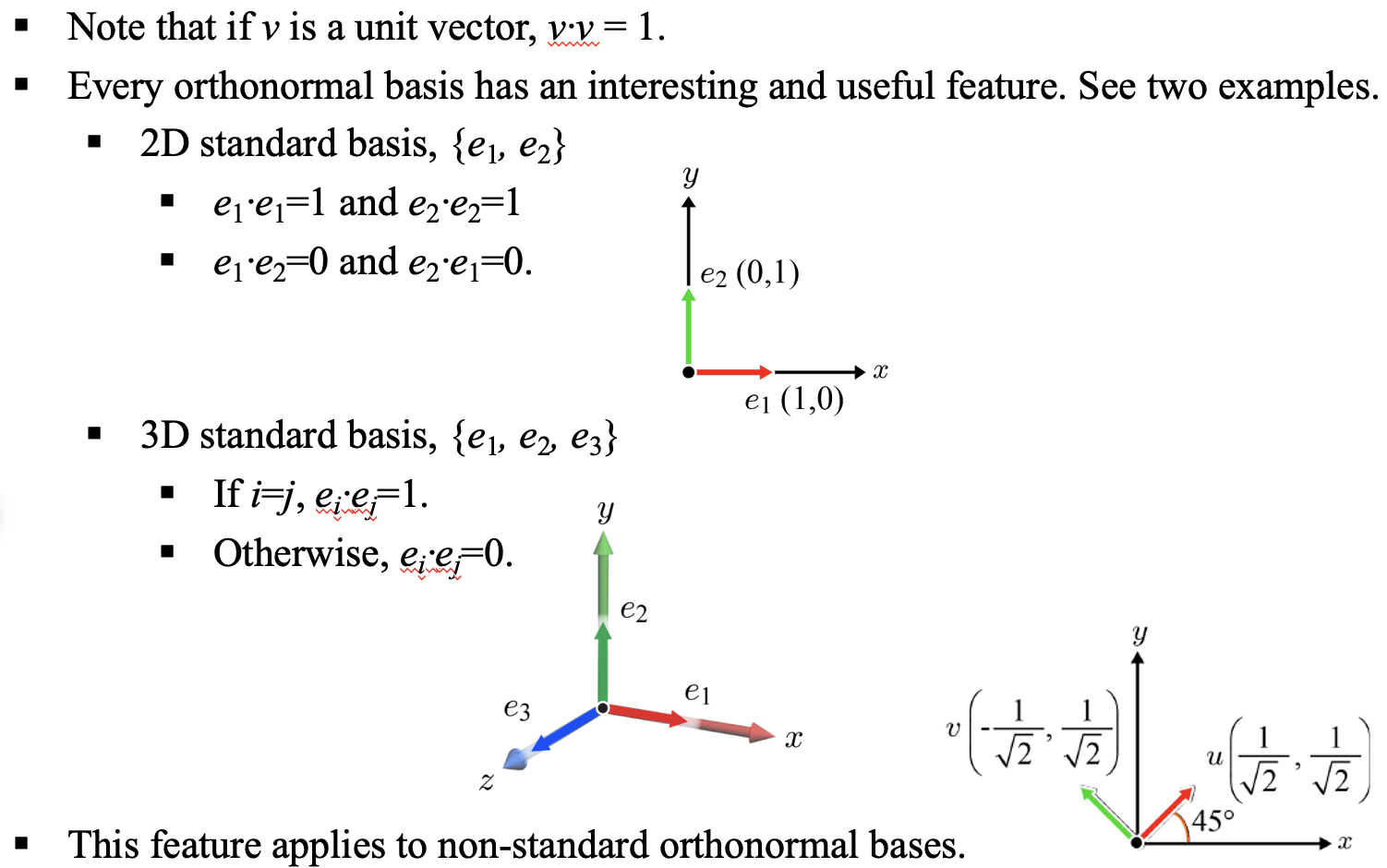
1. 단위벡터(unit vector) v를 자기자신과 내적시키면, ||v|| ||v|| cos0도가 된다. v의 크기와 cos0이 1 모두 1이기 때문에 1이 된다.
2. 1을 이용하면 orthonormal basis의 중요한 특징을 발견할 수 있다.
standard basis는 단위벡터이고 2개, 혹은 3개의 벡터가 서로 직교하기 때문에
2-1. 2D standard basis 에서 각각의 벡터는 자기 자신과 내적하면 1이되고, 두 벡터를 내적하면 0이 된다.
2-2. 3D standard basis 에서 각각의 벡터는 자기 자신과 내적하면 1이되고, 두 벡터를 선택하여 내적하면 0이 된다.
벡터 연산_Cross Product = Outer Product = 외적
외적의 결과값은 항상 벡터 값이 나온다.

1. 내적과 다르게 외적(Cross Product)은 3차원 벡터에서만 정의가 된다. 그 결과는 aXb 형태로 표현되고, 또다른 3차원 벡터값이 나온다. 결과로 나오는 벡터의 방향은 오른손 법칙을 따른다. 네 손가락이 a에서 b로 이동할 때, 엄지 손가락의 방향이 aXb의 방향.
2. aXb의 크기는 ‖a‖‖b‖sinθ, θ는 a와 b가 이루는 각도
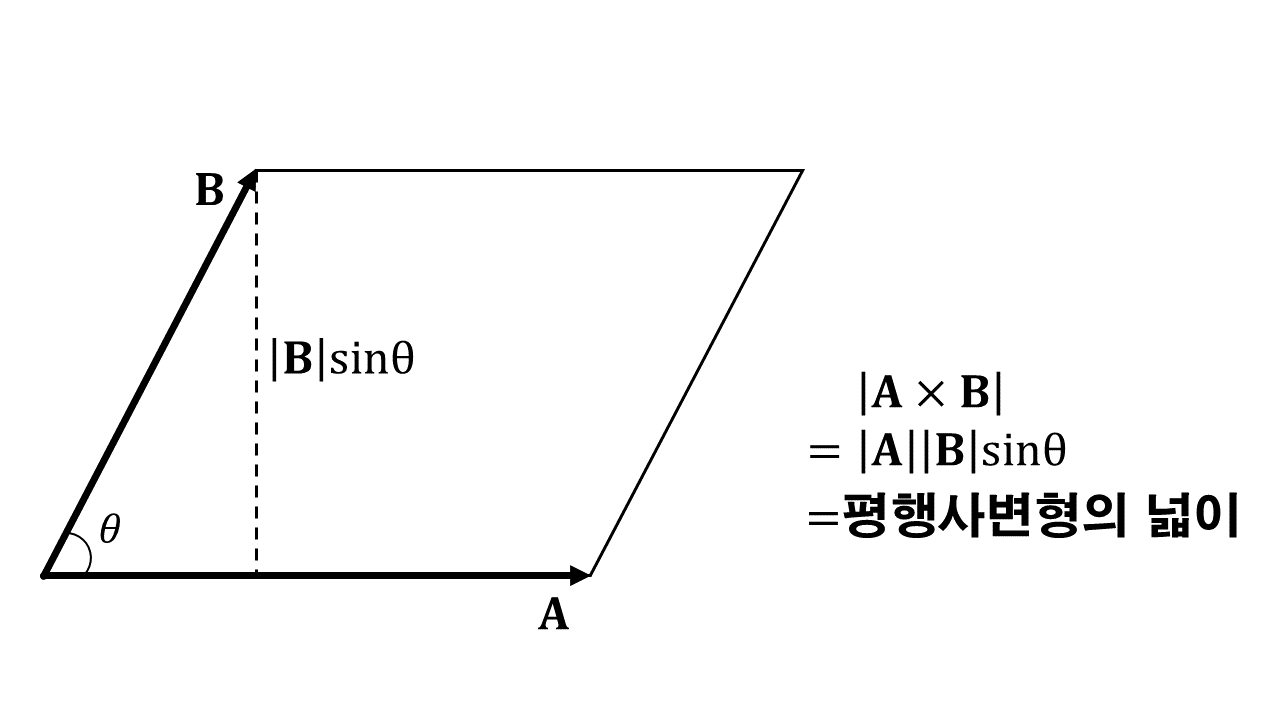
a벡터와 b벡터를 가만히 살펴보면 둘은 평행사변형을 이룬다. 평행사변형의 밑변의 길이는 a벡터의 길이가 되고 높이는 b벡터의 크기에 sinθ를 곱한 값이 된다. 밑변x높이 = a벡터의 크기*(b벡터의크기*sinθ)가 되는 것.
3. 이렇게 외적을 정의 했는데 만약 두 벡터가 a, b가 같다면 평행사변형의 면적은 어떻게 될까? 높이가 0이 되면서 0이 될 것이다.
aXb의 길이는 0이된다. aXb는 3차원 벡터이기 때문에 (x, y, z) 좌표가 모두 0인 zero vector를 만들어낸다.
4. 외적은 오른손 법칙이 적용되기 때문에, a와 b의 순서를 바꿔서 bXa를 하면 네 손가락이 b벡터에서 a벡터 방향으로 움직일 때, 엄지손가락의 방향이 된다(위의 2번째 그림에서는 엄지가 아래를 향함).
벡터의 크기는 두 벡터가 이루는 평행사변형의 면적과 같기 때문에 aXb와 같을 것이라고 쉽게 유추할 수 있다.

외적을 살펴봤는데, 실제적으로 aXb 라고 하는 3차원 벡터의 (x, y, z)좌표를 계산해야 한다.
빨간 걸로 표현된 것처럼
x좌표를 계산할 때는 a, b벡터의 x좌표를 배제하고 (a_y*b_z)-(a_z*b_y)를 한 게 결과 벡터의 x좌표가 된다.
마찬가지로 y좌표를 계산할 때는 a, b벡터의 y좌표를 배제하고 x좌표를 z좌표 옆에 두고 동일하게 계산한다.
z좌표 또한 a, b벡터의 z좌표를 배제하고 동일하게 계산한다.

p_0과 p_1 두 점이 주어졌을 때, 두 점을 잇는 직선을 생각할 수 있다. 이 직선을 어떻게 수식으로 표현할 수 있는가
p_0에서 p_1로 향하는 벡터는 p_1-p_0로 표현 할 수 있다.
그렇다면 두 점을 잇는 무한한 직선은 어떻게 표현할 수 있을까?(나중에 보고 이해가 안 될 수 있을 것 같아 남기는 타임라인)
1. t가 -∞~∞까지의 범위를 가진다고 할 때, 저 무한한 길이의 직선의 모든 점이 표현가능하다.
p_0과 p_t: p(t) = p_0+t(p_1-p_0) ←t에 0, 1 0.5를 대입해보면 이해가 쉬울 것 같다!
2. t의 범위가 [0,∞]일 경우, 그림상의 p_0에서 오른쪽 위로 무한히 이어지는 직선(ray라고 함)이 된다.
3. t의 범위가 [0,1]일 경우, 선분(line segment)이 만들어진다.
4. 1의 식 p_0+t(p_1-p_0)을 p_0로 묶으면, p_0+t(p_1-p_0)=p_0+(t*p_1)-(t*p_0*-1) = (1-t)*p_0 + t*p_1
p_0는 t가 0일 때고, p_1은 t가 1일 때이다. t가 0과 1 사이일 때 그 사이에 있는 점들을 모두 표현하는 것. 이런 점들은 양 끝점 p_0, p_1에 각각 가중치(1-t)와 t를 줌으로써 정의된다는 것.
즉, p_0와 p_1 사이에 있는 점은 양 끝점을 보간해서 만들 수 있다는 것. p_0와 p_1을 잇는 선분은 p_0과 p_1의 선형보간에 해당한다.
선분을 수학적 개념을 써서 표현한 것. 이러한 선형보간은 그래픽스에서 많이 쓰이는 개념.
이렇게 선형보간의 개념으로 선분을 이해했는데, 실제 우리가 2차원/3차원 공간이 주어졌을 때, 선형보간을 통해서 그 보간된 점의 x, y, z좌표를 계산해야 한다. 그것을 계산하는 것이 아래 식이다.
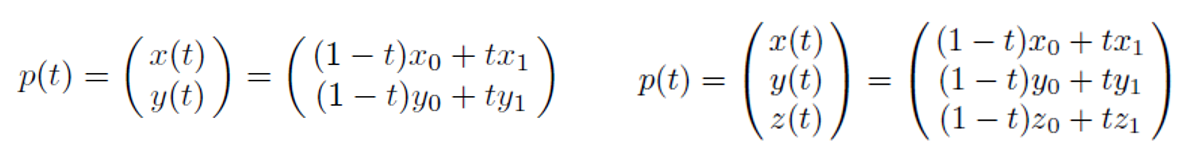
끝점과 연관된 속성이 무엇이든 선형 보간할 수 있습니다. 끝점이 각각 색상 c0 및 c1과 연관되어 있고, 여기서 c0 = (R0, G0, B0) 및 c1 = (R1, G1, B1)이라고 가정해 보겠습니다. 그러면 색상 c(t)는 다음과 같이 정의됩니다:
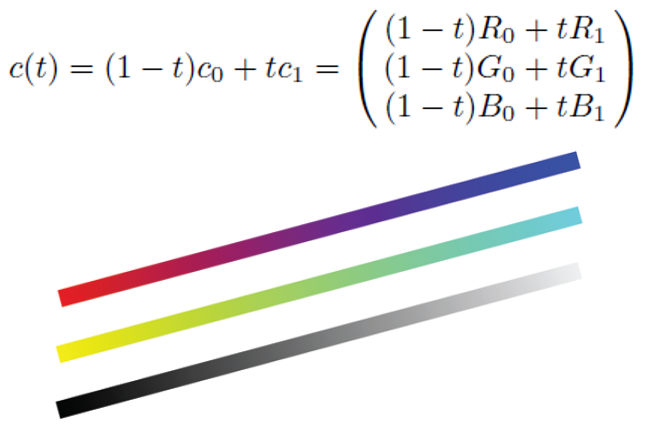
p_0, p_1이 끝점인 한 선분에 색상이라는 속성이 있다고 생각해보자.
색은 rgb로 표현이 되므로 p_0=c_0(R_0, G_0, B_0), p_1 =c_1(R_1, G_1, B_1)이라고 할 수 있다. 중간점들은 양 끝의 color 값을 보간해서 할당받을 수 있다. 보간을 위해서는 위에서 봤던 것과 같은 공식을 사용할 수 있다.
2장에서는 그래픽스에서 필요한 최소한의 기초 수학을 다뤄봤다. 3장에서는 3차원 그래픽스를 본격적으로 살펴본다.
'Programming > OpenGL' 카테고리의 다른 글
| [한정현 컴퓨터 그래픽스] 4장 좌표계와 변환 (0) | 2023.12.22 |
|---|---|
| [한정현 컴퓨터 그래픽스] 3장 모델링 (0) | 2023.12.20 |


