지우너
[한정현 컴퓨터 그래픽스] 3장 모델링 본문
본 글은 한정현 교수님의 "컴퓨터 그래픽스" 강의를 정리한 글입니다(강의에 사용된 ppt 링크).
모델링: 그래픽스에서 렌더링 할 어떤 물체를 만들어내는 것

위 그림의 구를 어떻게 정의할 것인지 생각해보자.
가장 간단한 방법은 구의 중점과 반지름을 갖고 구의 방정식으로 정의하는 것. 이런 것을 음함수(implicit function)라고 이야기한다. 문제는 gpu가 음함수를 처리하기에 적합하게 설계되어 있지 않다.
따라서 음함수 표현대신 부드러운 표면의 점을 샘플링(sample)한다. 그러면 일정한 갯수의 꼭짓점, 정점이 나온다. 이런 정점들을 보이는 것처럼 다각형으로 이어둔 것이 폴리곤 메쉬이다. GPU가 폴리곤 처리에 최적화되어 있기 때문에 폴리곤 메쉬 표현이 실시간 그래픽스에서 선호된다.

매끄러운 표면을 샘플링한 점을 이용해 만든 폴리곤 메쉬는 정확한 표현이 아니라 대략적인 표현임에 유의할 것.
그리고 폴리곤 중에서 가장 간단한 게 트라이앵글이다. 트라이앵글로만 구성된 폴리곤 메쉬를 트라이앵글 메쉬라고 부른다.
실제로 OpenGL ES는 일반적인 다각형을 처리하지 않고, 삼각형 메쉬만 처리한다. 삼각형 메쉬가 주어졌을 때 꼭지점 개수의 2배 정도 되는 삼각형이 있다(오일러 공식을 이용하여 증명할 수 있음).
일반적으로는 트라이앵글 메시가 훨씬 더 많이 사용되지만, 실제 모델링 단계(max나 maya등을 사용하는)에서는 쿼드 메시가 선호되는 경우가 많다. 모델링 단계에서 사각형 메쉬가 어떻게 쓰이는지 동영상을 보도록 하자
사각형 메쉬들의 정점들을 움직이고, 원래 있던 사각형을 잘게 분해하고 이런식으로 정규화된 모델을 만들어낸다.
모델링 기법자체를 이야기 하는 것이 아니라 보시는 것처럼 사각형 메쉬가 모델링 단계에서 널리 쓰인다는 것만 이해하면 될 것 같다.
max나 maya를 사용하여 사각형 메쉬가 만들어지면 삼각형 메쉬를 만드는 것은 간단하다. 사각형을 각각 두 개의 삼각형으로 나누면 된다.

사각형이건 삼각형이건 폴리곤 메쉬라고 하는 게 있으면 대체 정점의 개수를 어느 정도로 할 것인가.
화면에서 픽셀의 개수를 해상도(resolution)라고 한다. 마찬가지로 폴리곤 메쉬에서도 정점의 개수를 해상도 혹은 LOD(level of detail)라고 한다.

위 그림의 두 가지 예시를 보면 해상도가 변했을 때 어떤 장단점이 있는지 직관적으로 이해할 수 있다.
폴리곤 메쉬가 부드러운 표면을 sample해서 근사적으로 표현한 것이기 때문에 해상도가 높아질수록 당연히 원래 주어진 부드러운 표면에 가까워진다. 정확하게 모델링이 된다는 의미. 하지만 정점의 개수가 많아지므로 뭔가를 처리하는 데에 더 많은 시간이 걸린다.
어느 정도 해상도/LOD를 할지는 실제로 그 물체가 화면상에 어느 정도의 크기로 나올지에 따라 달라진다.
위 그림의 구가 화면 상에서 픽셀 10개 정도를 차지할 정도로 아주 작게 나온다고 생각해보자. 그러면 구의 정점 개수를 가장 오른쪽처럼 정확하게 샘플링하는 것은 오버하는 것. 2나 3정도로만 해도 구처럼 보일 수 있다(10px니까). 그런데 이 구를 향해 줌인을 한다고 생각하면 4정도로도 부족할 수 있다.
해상도를 늘리는 것을 refinement, 줄이는 것을 simplification이라고 하는데 이런 LOD 컨트롤이 그래픽스에서 중요한 주제 중 하나이다.
폴리곤 메쉬가 하나 주어졌다고 했을 때, 실제로 그 폴리곤 메쉬가 컴퓨터 안에서 어떤 식으로 표현이 될지 살펴보자.

위 그림의 2차원 메쉬는 삼각형이 3개 있고, 각각의 삼각형은 각각 3개의 정점에 의해 정의되어 있다.
이를 표현할 때
① △t1 (0, 0), (1, 0), (0, 1)
② △t2 (1, 0), (1, 1), (0, 1)
③ △t3 (1, 1), (1, 0), (2, 1) 이렇게 세 개의 꼭짓점을 배열에 적어둔다.
이렇게 모든 삼각형마다 정점을 배열에 계속 배치하고, 3개씩 끊어서 읽으면 삼각형 정보를 모두 얻을 수 있다.
vertex array: 삼각형을 구성하는 3개의 정점을 일렬로 나열해놓은 공간
→문제점: 중복된 데이터가 많다(=낭비가 심함). 위 그림에서 (1, 0)은 삼각형 3개가 공유하는 점, array에 3번 들어가게 된다.
<위 방법의 대안>

정점을 중복 없이 나열. vertex array를 사용하는데, 해당 메쉬는 5개의 정점을 갖고 있다. 5개만 array에 저장한다. 배열이니까 0번부터 시작. 왼쪽의 그림에서 각각의 정점을 0, 1, 2, 3, 4로 표기해두었다. 인덱스에 따라 idx array를 따로 하나 만들어둔다.
① △t1 (0, 0), (1, 0), (0, 1) ⇒ 해당 좌표가 저장된 vertext array의 인덱스 0, 2, 1을 idx array에 저장.
② △t2 (1, 0), (1, 1), (0, 1) ⇒ 해당 좌표가 저장된 vertext array의 인덱스 2, 3, 1을 idx array에 저장.
③ △t3 (1, 1), (1, 0), (2, 1) ⇒ 해당 좌표가 저장된 vertext array의 인덱스 3, 2, 4를 idx array에 저장.
위와 같이 vertex array+index array를 이용하는 것이 삼각형 메쉬를 표현하는 가장 일반적인 형태
vertex array만 사용한 방법은 9개의 원소를 저장하면 되는데, vertex array+index array는 9개의 원소+각각의 정점을 담는 array까지 필요하니까 낭비처럼 보인다.
⇒ 절대 아님!!!!! idx array의 원소들은 각각 2~4바이트 정도로 표현할 수 있는 정수. 아주 사이즈가 작다. 근데 vertex array의 원소는 (지금은 2차원 폴리곤 메쉬로 간단하게 예를 들었지만) 실제로는 (x, y, z) 3차원 좌표를 가지며, 각각은 실수값이다. 이는 vertex position에 불과하고, 그 밖에 여러 점보가 한 셀에 들어가게 되어 있다.
[어떤 정보가 들어갈지는 한 학기 동안 강의에서 배우게 된다! 배운 뒤 수정하여 채우기]
1. 정점의 position과 vertex normal
핵심은 이 vertex array의 한 셀이 엄청나게 크다는 것. 따라서 vertex array의 중복이 없도록 꼭짓점을 저장해서 얻을 수 있는 공간상의 이득은 index array가 야기하는 공간 상의 추가적인 요구보다 훨씬 더 크다!
∵ 삼각형 메쉬는 vertex array와 index array를 이용해서 표현
vertex array에는 position 외에도 여러 정보가 들어간다고 했다. 그 정보 중 하나가 지금 살펴볼 법선벡터(Normals)

먼저, 폴리곤 메쉬를 구성하는 각각의 삼각형마다 법선벡터를 어떻게 계산하는지 보자.
삼각형 <p1, p2, p3>이 주어졌을 때,
v1은 첫 번째 꼭짓점(p1)과 두 번째 꼭짓점(p2)을 연결하는 벡터
마찬가지로 v2는 첫 번째 꼭짓점(p1)과 세 번째 꼭짓점(p3)을 연결하는 벡터
이 두가지 벡터에 대해 오른손 법칙을 적용 → v1에서 v2로 4개의 손가락이 갈 때 엄지 손가락이 가리키는 방향이 외적(cross product)이 된다(v1 x v2).
외적의 중요한 성질: 입력으로 주어진 v1과 v2 두 벡터에 모두 수직인 벡터가 결과로 나온다.
결국 삼각형의 두 변에 수직인 벡터가 나온다는 이야기인데, 이는 삼각형에 수직인 벡터(=triangle normal)라고 할 수 있다.

컴퓨터 그래픽스에서는 모든 노멀을 다 단위벡터(길이가 1인 벡터, unit vector)로 표현한다. 그러기 위해 외적의 결과로 나온 벡터를 자신의 길이로 나누는 정규화(Normalization) 과정을 거쳐야 한다.
한 가지 신경써서 봐야 할 것은 삼각형을 p1, p2, p3라고 표현했는데, p1, p2, p3은 시계 반대 방향(CCW)으로 나열된다는 것.
그런데 삼각형의 꼭짓점이 <p1, p3, p2> (시계방향) 로 주어졌다고 생각해보자.

이 경우에도 앞에서 했던 것처럼 원칙을 적용해보자.
삼각형 <p1, p3, p2>이 주어졌을 때,
v1은 첫 번째 꼭짓점(p1)과 두 번째 꼭짓점(p2)을 연결하는 벡터
마찬가지로 v2는 첫 번째 꼭짓점(p1)과 세 번째 꼭짓점(p3)을 연결하는 벡터
이 두가지 벡터에 대해 오른손 법칙을 적용 → v2에서 v1로 4개의 손가락이 갈 때 엄지 손가락이 가리키는 방향이 외적(cross product)이 된다(v2 x v1).
앞페이지와 반대 방향을 가리키는 벡터가 나옴. 2장에서 배웠던 것처럼 외적의 방향은 두 벡터의 순서에 따라간다.
그러면 어떻게 해야 될까
<p1, p2, p3> 나 <p1, p3, p2>나 삼각형에 필요한 세 꼭지점을 나열한 것은 동일. 전자의 방식으로 정의하면 물체 바깥으로 나가는 법선이 정의되고, 후자의 방식으로 정의하면 물체 안쪽을 파고드는 법선이 정의된다.
⇒ 컴퓨터 그래픽스에서는 모든 법선이 물체의 바깥을 향하도록 원칙(=관례)을 정함
이 관례를 그대로 지키기 위해 반시계 방향으로 삼각형의 정점을 나열해야만 한다!!!
실제 예시를 한번 보자.

구에 두 삼각형 t1, t2를 보자.
우선 모든 정점을 vertex array에 저장한 후,
△ t1 <p, q, r> (반시계 방향으로 나열해야 함) → vertex array에 저장된 정점의 인덱스를 index array에 저장0, 1, 2
△ t2 <p, s, q> (마찬가지) → (마찬가지) 3, 1, 0
(△ t2 <q, p, s> 이렇게 해도 반시계 방향 index array에 3, 1, 0 대신 1, 0, 3이렇게 저장해도 유효하다!!)
삼각형 노말(triangle normal): 삼각형이라고 하는 표면에 수직인 법선
정점 노말(vertex normal): ?
triangle normal과 다르게 폴리곤 메쉬에서 정점마다 노말을 할당한다? 직관적으로 이해가 안 된다. 정점은 정점 하나. 법선은 이쪽일 수도 있고 저쪽일 수도 있지 않나?

매끄러운 표면을 샘플링해서 얻어진 것이 폴리곤 메쉬. 어떤 꼭짓점이 있다고 하면, 부드러운 평면의 점을 샘플한 것.
부드러운 평면에는 이른바 탄젠트 플레인이라고 하는 것을 수학적으로 정의할 수 있다. 탄젠트 플레인에 수직인 벡터가 normal이고, 얘네를 정점마다 할당해주면 된다.
폴리곤 메쉬에 정점마다 정점노말(vertex normal)을 할당하기 위해서는 부드러운 곡면이 항상 필요하다고 생각할 수 있다. 일견 맞는 말이지만 문제는 부드러운 메쉬 없이 오로지 폴리곤 메쉬만 주어진 경우가 굉장히 많다.
이렇게 폴리곤 메쉬 밖에 없을 때, 정점 노말을 어떻게 계산 할까.
각 정점은 여러 개의 삼각형에 의해 공유된다. 앞서 배운 것처럼 삼각형의 노말은 쉽게 계산할 수 있다. 그 정점을 공유하는 삼각형 노말의 평균을 내는 방식으로 정점 노말은 쉽게 계산할 수 있다.
그림 11의 아래쪽 그림을 보면 총 6개의 삼각형에 의해 빨간색 정점이 공유되고 있다. 6개 삼각형의 노말 n1~n6를 다 더하면 6개 벡터의 평균적인 방향이 나올 것이다. 이를 단위벡터로 만들어야 하니까 자기자신의 길이로 나누는 정규화 과정을 거친다.
(실은 프로그래머 입장에서는 max가 다 계산해주니까 걱정할 필요가 없다)
정점의 position과 normal 같은 것들이 정점 배열(vertex array)가 반드시 가져야 할 그런 정보.

캐릭터 메쉬 등을 유니티 같은 엔진이나, OpenGL ES로 렌더링 하기 위해서는 그 데이터를 끌어와야 한다.
그러기 위해 export(max 등에서 모델을 파일형태로 출력하는 것)와 import(유니티나 OpenGL ES 등에서 파일을 읽어들이는 것)의 과정을 거쳐야 함
3ds Max의 경우 MAXScript라고 하는 스크립트 언어를 이용해 export할 수 있다.
파일 포맷은 여러 가지를 지원하는데, 가장 많이 사용되는 형식은 .obj 파일이다.

간단한 구. 26개의 꼭짓점과 48개의 삼각형으로 정의되어있다(앞에서 삼각형의 갯수는 대체로 정점 갯수의 2배 정도라고 배움).
폴리곤 메쉬가 obj 파일에서 어떻게 구성이 되어 있는지 보자.
v(vertex의 약자)로 시작하는 줄들이 처음에 나온다. 뒤에 나오는 실수 값은 x, y, z 좌표.
이 폴리곤 메시는 26개 정점을 갖고 있기 때문에 v 로 시작하는 줄이 26개가 될 것.
정점 노말은 vn(vertex normal의 약자)으로 시작한다. normal이라고 하는 게 법선벡터이고, 3차원이니까 얘도 x, y, z 좌표를 가진다.
정점 노말도 26개. 구라는 특별한 경우니까 각각의 정점은 유니크한 노말을 가질 수밖에 없다. 그래서 26개 정점의 26개 노말이 저장되어 있는 것.
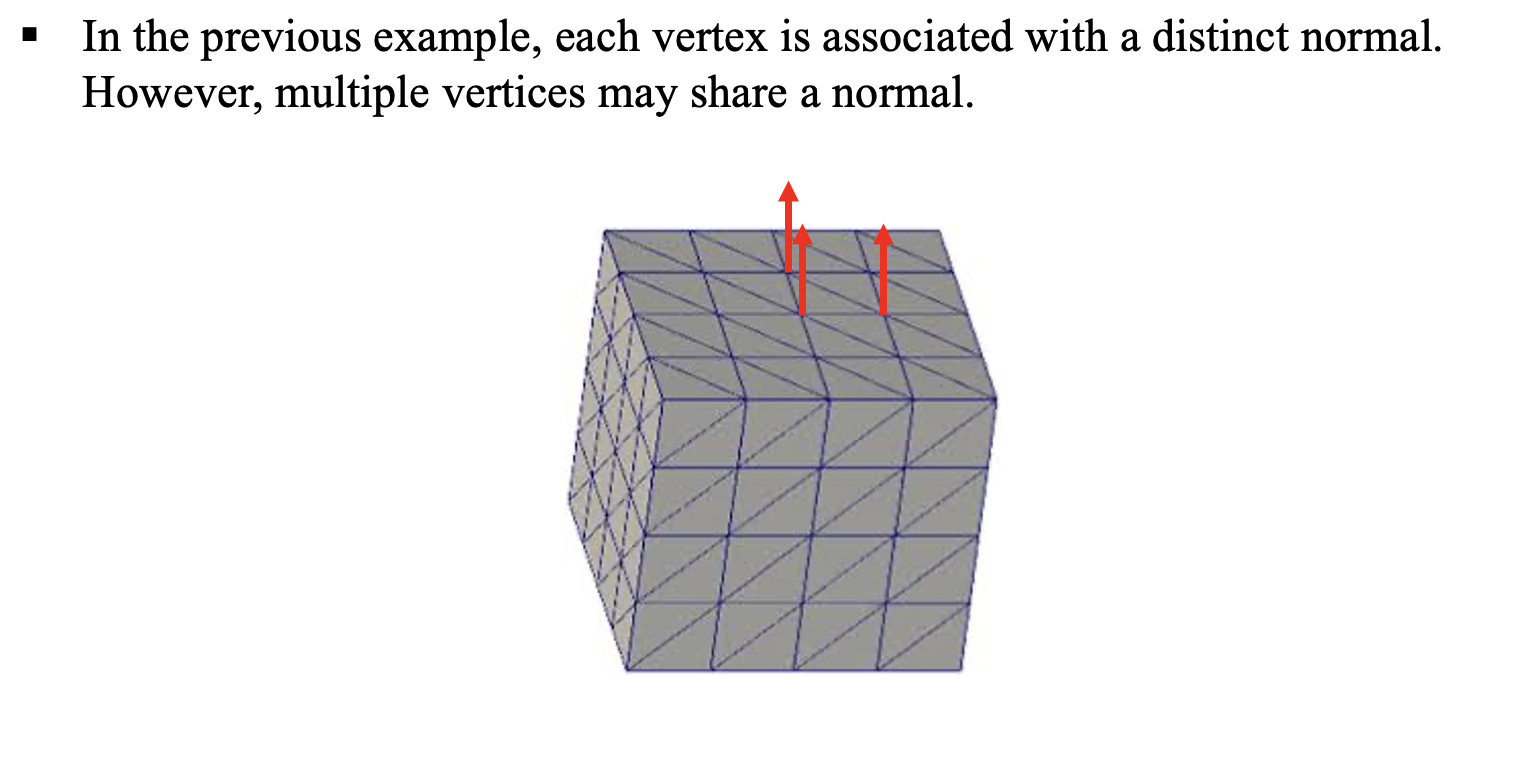
그런데 그림 14와 같은 박스를 우리가 모델링했다고 해보자.
표시된 정점의 position은 다르지만, 노말은 동일할 것이다. 이 경우 노말을 따로 저장하지 않고, 1개의 노말만 저장하면 된다.
'구'가 특별한 경우라고만 이해하고 넘어가자.
정점과 정점 노말을 그림 13에서 정리했으므로, 삼각형의 정보를 이제 줘야한다.
삼각형 정보는 f(face, 면의 약자)로 시작한다. 삼각형 메쉬 각 꼭짓점의 정보를 알려줘야 한다. 각각은 슬래시('/') 2개로 구분이 된 인덱스. vertex position, vertex normal의 인덱스 (1//1은 1번째 vertex position, 1번째 vertex normal이라는 의미)
맥스가 이런 obj 파일을 export한 것. import 과정에서는 삼각형들을 하나하나 읽는다. 각각 position, normal을 끌어올 수 있다.

이런 식으로 obj 파일을 계속 읽어나가면서 런타임 프로그램이 사용할 vertex array, index array를 채워 나가는 것
구 같은경우 26개 꼭지점이 있으니까 여기서 0부터 25까지 의 26개의 원소를 갖고 있는 vertex array 2개가 완성된다.
이 메쉬는 삼각형이 48개 있다. 각각의 삼각형이 3개의 정점을 갖고 있으니까 48삼각형*3개 정점 = 144개의 원소를 가진 index array가 나온다.
첫 번째 삼각형은 index 0, 1, 2 에 저장된 정점을 반시계방향으로 나열한 것.
렌더링 하려면 여러가지 작업들을 수행해야 되는데, 그중에 가장 먼저 해야 될 게 4장에서 다룰 변환이라는 것.
'Programming > OpenGL' 카테고리의 다른 글
| [한정현 컴퓨터 그래픽스] 4장 좌표계와 변환 (0) | 2023.12.22 |
|---|---|
| [한정현 컴퓨터 그래픽스] 강의소개, 1, 2강 (0) | 2023.12.19 |


